PEE-11

Free POLYTECHNIC notes on the internet For the first time by PRONAB BARUAH.
Send your comment on pronabengg@gmail.com

Explain what is series circuit ?

Ans.

     The circuit in which resistances are joined or connected end to end so that there is only one path for current flowing is called a series circuit.

Consider three resistance R₁, R₂ & R₃ ohms connected in series across a battery of V volt as shown in figure(i). 

    Obviously there is only one path for current I i.e., current is same throughout the circuit. By ohms law, voltage across the various resistance is………..

V₁ = IR₁ ;         V₂ = IR₂  ;        V₃ = IR₃

Now,

     V = V₁ + V₂ + V₃

     V = IR₁ + IR₂ + IR₃

     V = I ( R₁ + R₂ + R₃ )

 V/I = R₁ + R₂ + R₃

     But,   V/I   is the total resistance Rт between points A & B. Rт is called the total or equivalent resistance of the three resistances.

     So total resistance,  Rт =  R₁ + R₂ + R₃

     Hence, when a number of resistances are connected in series, the total resistance is equal to the sum of individual resistances.

PEE-10

Free POLYTECHNIC  notes on the internet for the first time by PRONAB BARUAH.

Send your comment on pronabengg@gmail.com

What is temperature co-efficient of resistance? Derive an expression for temperature co-efficient of resistance.

Ans.

     The change of resistance of a material with temperature is expressed by means of temperature co-efficient of resistance.

     Let a conductor having initial resistance Rₒ at 0 ⁰C and Rᵼ be the final resistance at t ⁰C.

So increase in temperature……………

                                                            ΔR = Rt- Rₒ

     This increase in resistance is…………

(a) directly proportional to its initial resistance i.e., Rt- Rₒ ∝  Rₒ

(b) directly proportional to the rise in temperature i.e., Rt- Rₒ ∝  t

(c ) depends upon the nature of the material.

     Combining first two we get,

                                                Rt- Rₒ ∝  Rₒt

                                                 Rt- Rₒ = αₒRₒt ……………………….. (i)

     Where αₒ is a constant & is called temperature co-efficient of resistance at 0 ⁰C. Its value depends upon the nature of material and temperature.

     Rearranging equation ( i ), we get,

                                                            Rt = Rₒ + αₒRₒt

                                                                 = Rₒ( 1 + αₒt) …………………. (ii)

     So temperature co-efficient of resistance is expressed as given below from equation (i)..........

                        αₒ = Rt- Rₒ/ Rₒt

                             = Increase in resistance/ohm original resistance/⁰C rise in temperature

Hence, temperature co-efficient of resistance of a material is the increase in resistance per ohm original resistance per ⁰C rise in temperature.

     If a conductor has a resistance Rₒ, R₁ & R₂ at 0 ⁰C, t₁ ⁰C  & t₂ ⁰C respectively, then…..

R₁ - Rₒ = α Rₒ t₁

       R₁ = Rₒ + α Rₒ t₁

        R₁ = Rₒ(1 + αt₁) ……………. (iii)

 R₂ - Rₒ = α Rₒ t₂

       R₂ =  Rₒ + α Rₒ t₂

       R₂ =  Rₒ(1 + αt₂) …………..(iv)

Dividing equation (iv) by equation (iii), we get….

    R₂/R₁ = Rₒ(1 + αt₂)/ Rₒ(1 + αt₁)

   R₂/R₁ = (1 + αt₂)/(1 + αt₁)

●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●

PEE-9

Free POLYTECHNIC notes on internet For the first time by PRONAB BARUAH. Send your comment on pronabengg@gmail.com

What is conductance ? Give the unit of conductivity .

Ans.

        Conductance(G) is reciprocal of resistance. Whereas resistance of a conductor measures the opposition which it offers to the flow of current, the conductance measures the inducement which it offers to flow of current.

We have   R = þ( L/A )   , R = þ

               Conductance, G = 1/R

                                     G = 1/ (þ L/A )

                                     G = A/ þ L            ( Since, 1/ þ  = σ )

                     So,           G =   σ A/L

Where σ ( Greek letter sigma ) is called the conductivity or specific conductance of the material. The unit of conductance is mho i.e., ohm spelt backward.

     So the unit of conductivity, σ = (mho × metre)/(square metre)

                                                          = mho/metre

     The above little reflection shows that SI unit of conductivity is mho/metre . Now-a-days, the siemen (s) is used as the unit of conductance & conductivity is expressed as siemen/metre.

What are the effects of temperature on resistance ?

Ans.

        Generally, the resistance of a material changes with the change in temperature. The effect of temperature on resistance can be written as follow……….

(a) If the resistance of a pure metal or a conductor increases, the resistance of the conductor varies directly.

     So metals have positive temperature co-efficient of resistance. Graphically it can be shown as below..........

(b) If the temperature of a semiconductors, electrolytes, insulators etc increases, the resistance of these substance decreases. Hence these materials have negative temperature co-efficient of resistance.

(c) In case of alloys, if the temperature increases, the increases in resistance is relatively small and irregular. For some high resistance alloys (example, Eureka, manganin, constantan etc), the change in resistance is practically negligible over a wide range of temperatures.

      

PEE-8

Free POLYTECHNIC notes on internet For the first time by PRONAB BARUAH

Define resistance ? Explain the laws of resistance & give the unit of resistivity.

Ans.

         It may be derfine as the property of a substance due to which it opposes the flow of electricity through it.

          Unit of resistance

                                              V ∝  I

                                         V = R I

                                         R = V/ I    volt/ampere    = ohm (Ω)

 Laws of resistance are explained below……………….

      The resistance of a conductor depends on the following factors :-

(a) LENGTH :-       The resistance  of a conductor is directly proportional to its length i.e., R  ∝  L  ( R= resistance, L = length )

(b) CROSS-SECTIONAL  AREA :- The resistance of a conductor is inversely proportional to its  cross-sectional area i.e.,  R ∝  (1/A)

(c) NATURE OF THE MATERIAL :- It depends upon the nature of the material. As different material  offers  different resistance to the flow of electricity.

(d) TEMPERATURE :- Resistance depends upon the temperature of the conductor i.e., if the temperature of a conductor increases, resistance directly varies ; In case of semi-conductor if the temperature increases, resistance inversely varies.

     Neglecting the last factor ( temperature ) we have……….

                                                                                                  R ∝  (L/A)

                                                                                                   R = þ(L/A)…….(i)

     Where  þ is constant and is known as specific resistance or resistivity, it depends on the nature of the material.

     Now we putting in equation (i)………..  L = 1 meter & A = 1 m²

                                                              Then, R = þ( L/A )

                                                                             = þ (1/1)

                                                                           R = þ

Unit of resistivity :-

     We know that  R ∝  (L/A)

                                 R = þ( L/A )

                                 Þ = RA/L

     Hence the unit of resistivity will be depend upon the unit of area of cross-section (A) & length (L).

     If the length is measured in metres and area of cross-section in square metres, then the unit of resistivity will be ohm-metre (Ω-m) i.e.,

                                                                       R = þ( L/A )

                                                                       Þ = RA/L

                                                                           = ohm×m²/m

                                                                   Þ  = ohm-m

PEE-7

Explain the term induced emf?

Ans :-

         Whenever magnetic flux linked with the coil changes, an emf is always induced in it . This change in magnetic flux can be brought in the following two ways……………..

(a) If the conductor is moved in a stationary magnetic field in such a way that the magnetic flux linked with it changes in magnitude. Then, the emf induced in this way is called dynamically induced emf.

(b) If the conductor is stationary and the magnetic field is moving or changing. The emf induced in this way is called statically induced emf. It is so called because the emf induced in the conductor which is stationary .

     A statically induced emf is further sub-divided into……..

(i) Self-induced emf & (ii) Mutually-induced emf

How an induced emf is produced dynamically on a uniform magnetic field, explain ?

Ans :-

        If a conductor is moved in a uniform ( stationary ) magnetic field in such a way that the magnetic flux linked with it changes in magnitude, then the induced emf is known as dynamically induced emf .

     Dynamically induced emf is illustrated with the help of following figure.....

       Consider a single conductor A of length L meters and let, it is moving at right angles to a uniform magnetic field of flux density B wb/m² with a velocity V m/s as shown in the figure. Suppose the conductor moves through a small distance dx in time dt. Then area swept by the conductor is =?(L) × (dx) m²

So magnetic flux cut, (dØ) = Flux density × area swept

                                                = BLdx wb

Change in flux ( dØ ) = BLdx wb

Time taken                  = dt

     According to Faraday’s law of electromagnetic induction, emf induced e in the conductor (A) is equal to rate of change of flux linkages.

e = NdØ/dt

e = BLdx/dt  =BL( dx/dt)           [ where, N = 1 & dx/dt  = v  ]

e = BLv    volts

      If the conductor moves at an angle θ  to the magnetic field, then the induced emf is given, e = BLvsinθ  . The direction of induced emf can be determined by Fleming’s right-hand rule.

What is self induced emf ?

Ans :-

        When a current is flow through a coil, a magnetic field is established through the coil itself. If the current in the coil changes, the magnetic field ( flux ) linked with the coil also changes and an emf is induced in the coil. This emf is known as self-induced emf. The magnitude of this self induced emf is equal to the rate of change of magnetic flux linked with the coil, i.e.,

                                                             e = N(d∅/dt)  volts

      The direction of self induced emf can be found by Lenz’s law. According to this law the induced current flows in such a direction that the action of magnetic field set up by it tends to oppose the very cause which produces it.

    

     It should be noted here that self induced emf exist in the coil when the current in the coil changes. When current in the coil steady or constant the magnetic field also becomes constant and there will be no existence of self induced emf in the coil.

     It should be noted here that self induced emf exist in the coil when the current in the coil changes. When current in the coil steady or constant the magnetic field also becomes constant and there will be no existence of self induced emf in the coil.

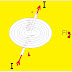
What is mutually induced emf ?

Ans :-

       The emf induced in a coil due to the changing current in the neighbouring coil is called mutually induced emf.

      Consider two coils A & B placed adjacent to each other as shown in the above figure. A part of the magnetic flux produced by coil A due to the changing current links with coil B. As the current in the coil A changes, flux linked with coil B is also changes. Hence a mutually induced emf is produced in coil B. 

     The magnitude of mutually induced emf is given by Faraday’s law and the direction of mutually induced is given by Lenz’s law.

     The mutually induced emf in coil B exist as long as the change of current in coil A continues. If the current in coil A becomes constant, the mutual flux also becomes steady and so no mutually induced emf in coil B.